# Write a function named, rollDice that simulates the rolling of one or
# more dice.
#
# - The function should take a single argument, numberOfDice that indicates the
# number of dice being thrown.
#
# - numberOfDice is expected to be a positive whole number.
# If it is not then the function should stop and display an
# error message.
#
# - The function should return a vector of random whole numbers.
# The value of each number should be randomly chosen to be 1,2,3,4,5 or 6.
# There should be as many numbers in the vector as indicated by the
# argument numberOfDice.
#
# For example:
# > rollDice(1)
# [1] 3
#
# > rollDice(1)
# [1] 6
#
# > rollDice(2)
# [1] 2 4
#
# > rollDice(2)
# [1] 6 1
#
# > rollDice(5)
# [1] 6 3 3 4 6
#
# > rollDice(5)
# [1] 4 4 2 6 5
#
#
# PART A
#
# Use the sample function to write rollDice.
#
#
# PART B
#
# Instead of the sample function, use the runif function (see ?runif).
# Set the min and max arguments of runif to 1 and 7 respectively.
# Then use the trunc function to remove the decimal points from the
# values that runif returns. Using this approach it will be
# impossible for the code to result in anything other than
# 1,2,3,4,5 or 6. runif will NOT generate a 7 since
# the documentation for runif says the following:
#
# runif will not generate either of the extreme values unless
# max = min or max-min is small compared to min, and in particular
# not for the default arguments.
#
# Therefore once you truncate the result that you get from runif you
# will be left with numbers that are either 1,2,3,4,5 or 6.
#
#
# PART C (THINKING DEEPER)
#
# If you follow the hints above, for part B, the resulting rollDice function,
# is not 100% "fair". Note that according to the documentation mentioned above
# if you specify min as 1 and max as 7, then runif will never generate 7.0000
# or 1.00000. Therefore, technically, the result of your rollDice function
# would be very slightly less likely to generate 1s than other numbers.
# Think about how you could theoretically fix this - One way is that you could
# set min to 0 (zero) and max to 7 and then truncate the result with trunc.
# If you get a zero, you keep repeating this process until you got a
# number that wasn't 0. 43 Practice Questions - TOPIC: loops (writing code)
QUESTION 1 - TOPICS: generating random values
QUESTION 2 - TOPICS: loops, cat vs return
# NOTE: You must answer the previous question before doing this one.
#
# Write a function named keepRollingUntilSnakeEyes.
#
# - The function should not take ANY parameters.
#
# - The function should keep calling rollDice(2) inside of a loop to
# simulate multiple rolls of two dice.
#
# - The loop should stop when the roll is two ones (i.e. "snake eyes").
#
# - The function should display the values each roll as shown below.
#
# - The function should return the total number of rolls that were made.
#
# - See the examples below.
#
# HINTS:
# a. Use the cat function to display the messages.
# b. Use a variable to keep track of how many rolls took place
# c. keep looping until you get a 1 and a 1
#
# EXAMPLES:
#
# Note that in the first two examples below, the last value displayed is the
# value that is "returned".
# In the third example below, the return value is captured in a variable
# and is displayed in a separate command. (also see the next question).
#
# > keepRollingUntilSnakeEyes() # return value appears after all the messages
# roll #1 was: 2 and 1
# roll #2 was: 3 and 5
# roll #3 was: 6 and 5
# roll #4 was: 4 and 1
# roll #5 was: 5 and 5
# roll #6 was: 6 and 1
# roll #7 was: 2 and 3
# roll #8 was: 6 and 3
# roll #9 was: 5 and 4
# roll #10 was: 6 and 3
# roll #11 was: 6 and 3
# roll #12 was: 4 and 5
# roll #13 was: 4 and 1
# roll #14 was: 4 and 2
# roll #15 was: 1 and 1
# [1] 15
#
# > keepRollingUntilSnakeEyes() # return value appears after all messages
# roll #1 was: 1 and 1
# [1] 1
#
# > numRolls <- keepRollingUntilSnakeEyes() # return value captured in numRolls
# roll #1 was: 2 and 1
# roll #2 was: 4 and 3
# roll #3 was: 3 and 6
# roll #4 was: 3 and 6
# roll #5 was: 4 and 3
# roll #6 was: 6 and 4
# roll #7 was: 6 and 2
# roll #8 was: 3 and 2
# roll #9 was: 4 and 1
# roll #10 was: 1 and 1
#
# > numRolls # This is the value that was returned from the function
# [1] 10QUESTION 3 - TOPICS: loops
# Modify the function that you created in the previous question,
# keepRollingUntilSnakeEyes. In this new version you should define a single
# argument named, showOutput. The default value of showOutput should be FALSE.
# If showOutput is TRUE then the messages should be displayed.
# If showOutput is FALSE then the messages should NOT be displayed.
# In either case, as with the last question, the function should return
# total number of rolls. For example:
#
# EXAMPLES:
#
# > keepRollingUntilSnakeEyes() # this will not show output
# [1] 48
#
# > keepRollingUntilSnakeEyes(showOutput = FALSE) # nor will this
# [1] 80
#
# > keepRollingUntilSnakeEyes(FALSE) # nor will this
# [1] 1
#
# > keepRollingUntilSnakeEyes(TRUE) # this WILL show output
# roll #1 was: 4 and 4
# roll #2 was: 4 and 6
# roll #3 was: 5 and 4
# roll #4 was: 4 and 3
# roll #5 was: 5 and 6
# roll #6 was: 5 and 5
# roll #7 was: 2 and 3
# roll #8 was: 3 and 1
# roll #9 was: 1 and 3
# roll #10 was: 3 and 4
# roll #11 was: 3 and 2
# roll #12 was: 1 and 2
# roll #13 was: 6 and 3
# roll #14 was: 1 and 1
# [1] 14
#
# > keepRollingUntilSnakeEyes(showOutput = TRUE) # this WILL show output
# roll #1 was: 2 and 4
# roll #2 was: 6 and 1
# roll #3 was: 4 and 2
# roll #4 was: 5 and 4
# roll #5 was: 5 and 6
# roll #6 was: 1 and 1
# [1] 6QUESTION 4 - TOPICS - loops
# NOTE: You must answer the previous questions before doing this one.
#
# Do all of the following steps:
#
# PART A
#
# Write a function named playManyTimes that calls the function
# keepRollingUntilSnakeEyes in a loop.
# The function playManyTimes should take an argument, n, that indicates the
# number of times the game should be played. playManyTimes should return a
# vector that contains the number of rolls it took each time the
# keepRollingUntilSnakesEyes function was called. For example:
#
# > playManyTimes(3)
# [1] 66 1 22
#
# > playManyTimes(10)
# [1] 6 27 35 106 38 51 100 1 1 26
#
#
# PART B
#
# Run the command: results <- playManyTimes(10000)
# to capture the results of playing the game ten thousand times.
#
# PART C
#
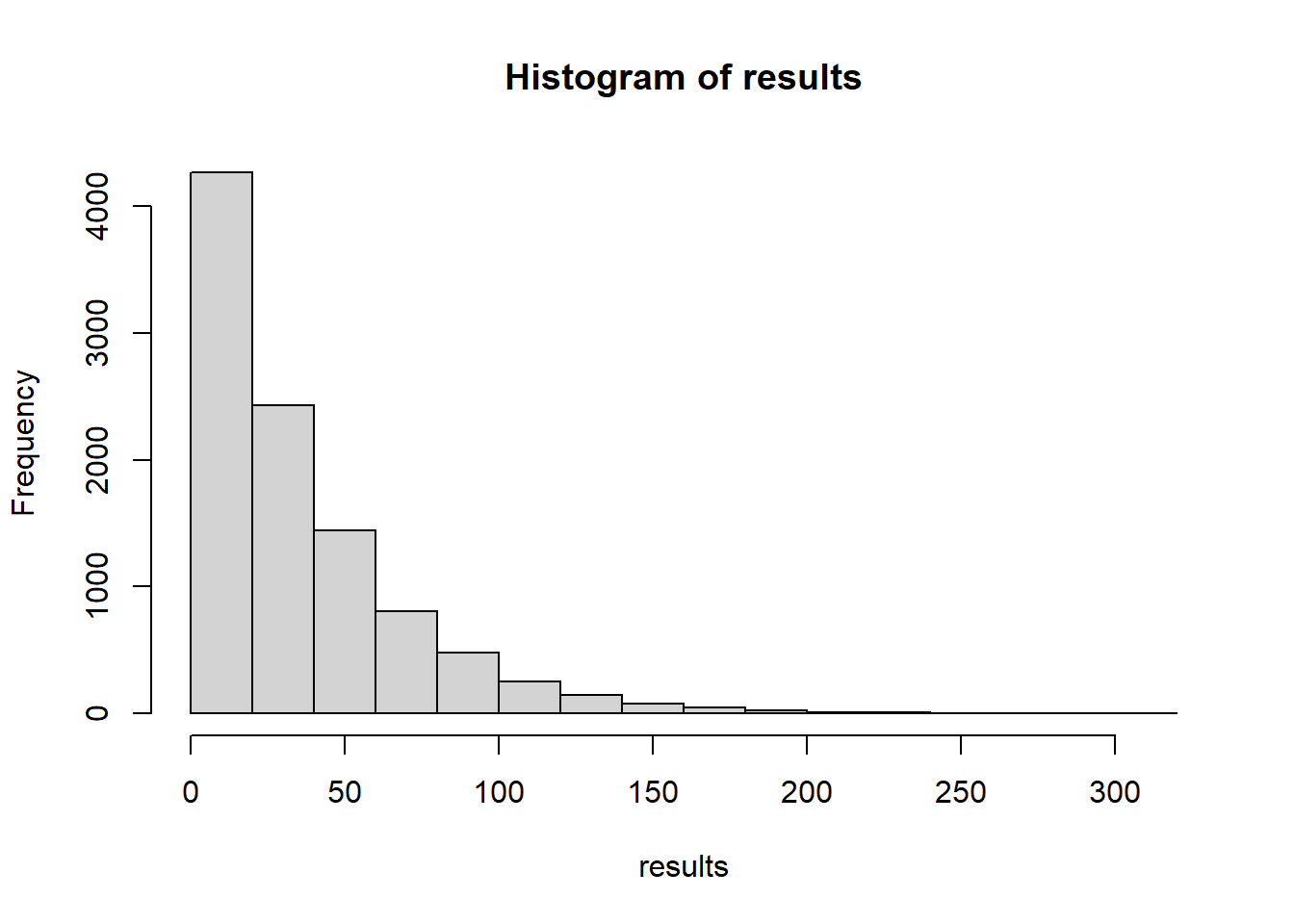
# Create a histogram of the results with the command: h <- hist(results)
# The histogram should look similar to the example shown below. You can see
# from this histogram that the function keepRollingUntilSnakeEyes
# is much more likely to return smaller numbers than to return larger
# numbers:
#
#
# PART D
#
# In the previous step the command: h <- hist(results)
# displayed a histogram. However, the function also returned an R "list"
# that was captured in the variable h. The value of the list wasn't
# displayed since hist returns an "invisible" value (see ?invisible)
# In any case, even though the return value is "invisible" you can still
# display the contents of this variable to examine details about
# the histogram (see the output below).
#
# For example, the counts entry in h contains the number of values in the
# results variable that fell into each "bar" of the histogram.
# The sum of all these counts are 10,000,as should be expected.
#
# Examine the value of the counts entry in the list.
# Then use the sum function to check to make sure that the
# counts sum to a total of 10,000 (as they should).QUESTION 5 - TOPICS: loops, if/elseif/else, cat vs return
# The game of "craps" involves a player rolling a pair of dice repeatedly
# according to the rules shown below.
#
# a. The first roll:
# i. If the player rolls 7 or 11 he/she wins
# ii. If the player rolls 2, 3 or 12, he/she loses
# iii. if the player rolls any other number, that number becomes the "point"
#
# b. All other rolls
# i. If the player hasn't won or lost on the first roll, then the
# player keeps rolling until either he rolls a 7 or
# the "point" (i.e. the same value as the very first roll).
# If the player rolls a 7 he loses.
# If the player rolls the "point" he wins.
#
# Write a function named, playCraps, that simulates the computer
# playing a single game of craps. The function should return TRUE if
# the player wins the simulated game and FALSE if the player loses the game.
#
# Define a single argument named, showOutput. The default value of showOutput
# should be FALSE. If showOutput is TRUE then the messages should be displayed.
# If showOutput is FALSE then the messages should NOT be displayed.
# In either case, the function, playCraps, should return TRUE if the player
# wins and FALSE if the player loses. For example:
#
# EXAMPLE 1 (showOutput is FALSE):
#
# > playCraps(showOutput = FALSE)
# [1] FALSE
#
# > playCraps(showOutput = FALSE)
# [1] TRUE
#
# > playCraps(showOutput = FALSE)
# [1] FALSE
#
# > playCraps(showOutput = FALSE)
# [1] TRUE
#
# EXAMPLE 2 (showOutput is TRUE):
#
# > playCraps(showOutput = TRUE)
# roll #1: 7
# WIN
# [1] TRUE
#
# > playCraps(showOutput = TRUE)
# roll #1: 12
# LOSE
# [1] FALSE
#
# > playCraps(showOutput = TRUE)
# roll #1: 6
# roll #2: 11
# roll #3: 5
# roll #4: 5
# roll #5: 6
# WIN
# [1] TRUE
#
# > playCraps(showOutput = TRUE)
# roll #1: 6
# roll #2: 9
# roll #3: 5
# roll #4: 9
# roll #5: 4
# roll #6: 4
# roll #7: 9
# roll #8: 3
# roll #9: 3
# roll #10: 2
# roll #11: 4
# roll #12: 8
# roll #13: 10
# roll #14: 7
# LOSEQUESTION 6 - TOPICS: loops
###########.
# PART A
###########.
# We can simulate playing craps many, many times. This can be done to
# generate an estimate the probability of winning a game of craps.
#
# Do the following:
#
# a. Create a function, playCrapsManyTimes, that takes a single argument, n.
#
# b. The function should return a vector that contains the results of calling
# the playCraps command n times.
#
# c. Use the function to simulate playing craps ten thousand times
#
# d. Calculate the percent of times that the player won the game
# (i.e. total TRUEs divided by total number of games played).
# Since TRUE is treated as 1 and FALSE as zero, it is possible to use
# the mean function to calculate this.
#
# e. For example the following shows that there is only
# approximately a 47.9% chance of winning the game of craps.:
#
# > results <- playCrapsManyTimes(10000)
# > mean(results)
# [1] 0.47915
#
# The more times we play, the more accurate our estimate of the
# probablily of winning will be.